[Dayilmu.blogspot.com]

Kalian masih ingat film serial kera sakti, sun go kong? Dalam film tersebut sang Biksu Tong sham chong sering berucap
Isi adalah kosong,kosong adalah isi
Saya akan menjelaskan maksud dari perkataannya secara matematika.
Himpunan
Himpunan adalah kumpulan2 objek yang sejenis dinotasikan dengan kurung buka dan tutup kurawal {}, contoh A={a,b,c} artinya himpunan A berisikan/berelemenkan a,b dan c
(Note: Disini saya menuliskan himpunan dengan huruf kapital dan elemen dengan huruf kecil)
Dengan mudah diketahui himpunan A mempunyai banyak anggota atau kardinalitas 3 dinotasikan |A|=3.
Himpunan juga bisa berisikan himpunan contoh D={B,C} misalkan B={1,2} dan C={3,4} maka D={{1,2}{3,4}}. Andaikan kita punya himpunan E={1,2,3,4} pertanyaannya
Apakah himpunan D dan E sama ? Apakah {{1,2}{3,4}}={1,2,3,4}?
TIDAK.. himpunan D berelemenkan himpunan {1,2} dan {3,4} sedangkan E berelemenkan 1,2,3 dan 4. Jadi {1,2},{3,4} adalah himpunan sedangkan 1,2,3,4 merupakan elemean. Untuk lebih jelasnya lagi 1 dan {1} berbeda karena 1 adalah elemen dan {1} adalah himpunan
Sekarang misalkan kita punya himpunan {a},{{a}} dan { {{a}} }
Apakah {a}={{a}}={{{a}}}?
Tentu tidak {a} berelemenkan a , {{a}} berelemankan himpunan {a}. dan { {{a}} } berelemenkan himpunan {{a}}. Selanjutnya kita peroleh:
|{a}|=1
|{ a,{a} }|=2
|{ a,{a},{{a}} }|=3
|{ a.{a},{{a}},{{{a}}} }|=4
karena {a}≠{{a}}}≠{{{a}}}
Himpunan juga boleh tidak mempunyai isi atau elemen, yang disebut himpunan kosong yang dinotasikan {Ø} dengan |{Ø}|=0
nah sekarang apakah {Ø}={{Ø}}?
Tentu saja tidak {Ø} himpunan kosong sedangkan {{Ø}} himpunan berelemenkan {Ø} itu artinya |{{Ø}}|=1
nah sekarang kita peroleh
{Ø} → 0
{{Ø}} → 1
{ {Ø},{{Ø}} } → 2
{ {Ø},{{Ø}},{{{Ø}}} } → 3
{ {Ø},{{Ø}},{{{Ø}}},{{{{Ø}}}} } → 4
.
.
.
.
{ {Ø},{{Ø}},{{{Ø}}},{{{{Ø}}}}…… } → n
Jadi menurut matematika kita bisa membuat/mengkontruksikan himpunan yang tak hingga banyaknya padahal himpunan tersebut sebenarnya kosong. Dengan matematika kita bisa membuat yang kosong menjadi tak hingga banyaknya padahal yang tak hingga banyaknya tersebut adalah kosong.
Nah sekarang kalian mengertikan makna dari “isi adalah kosong, kosong adalah isi”
atau kalian malah bingung
———————————————————————————————————————————————-r
Boleh dibilang ini adalah lanjutan dari part sebelumnya, saya akan melanjutkan bagaimana matematika memandang konsep “isi adalah kosong, kosong adalah isi”. Nah..pernahkah kalian bertanya/berpikir
Berapa sich hasil penjumlahan dari SEMUA bilangan real?
atau dengan kata lain
Berapa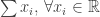 ?
?
Bagaimana kalo saya bilang hasilnya nol. Yup..semua bilangan kalo dijumlahkan hasilnya adalah nol.
Lho kok bisa?
Kita tahu bahwa himpunan bilangan real merupakan gabungan dari himpunan bilangan positif, himpunan bilangan negatif, dan singleton nol

denagan himpunan bilangan positif dan himpunan bilangan positif. Nah sekarang jumlahkan semua bilangan didalam himpunan bilangan positif , lalu jumlahkan juga semua bilangan didalam himpunan bilangan negatif
, lalu jumlahkan juga semua bilangan didalam himpunan bilangan negatif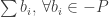 , maka dengan mudah kita ketahui
, maka dengan mudah kita ketahui

atau dengan cara yang lebih sederhana akan saya tulis

***
Didalam teori himpunan nol menunjukan banyaknya elemen didalam himpunan kosong . Nol merupakan cerminan dari kosong, telah kita tunjukan nol merupakan
jumlah total dari semua bilangan. Itu berarti secara filosofi kosong
sebenarnya merupakan penggabungan total semua hal/isi.
. Nol merupakan cerminan dari kosong, telah kita tunjukan nol merupakan
jumlah total dari semua bilangan. Itu berarti secara filosofi kosong
sebenarnya merupakan penggabungan total semua hal/isi.

Kalian masih ingat film serial kera sakti, sun go kong? Dalam film tersebut sang Biksu Tong sham chong sering berucap
Isi adalah kosong,kosong adalah isi
Saya akan menjelaskan maksud dari perkataannya secara matematika.
Himpunan
Himpunan adalah kumpulan2 objek yang sejenis dinotasikan dengan kurung buka dan tutup kurawal {}, contoh A={a,b,c} artinya himpunan A berisikan/berelemenkan a,b dan c
(Note: Disini saya menuliskan himpunan dengan huruf kapital dan elemen dengan huruf kecil)
Dengan mudah diketahui himpunan A mempunyai banyak anggota atau kardinalitas 3 dinotasikan |A|=3.
Himpunan juga bisa berisikan himpunan contoh D={B,C} misalkan B={1,2} dan C={3,4} maka D={{1,2}{3,4}}. Andaikan kita punya himpunan E={1,2,3,4} pertanyaannya
Apakah himpunan D dan E sama ? Apakah {{1,2}{3,4}}={1,2,3,4}?
TIDAK.. himpunan D berelemenkan himpunan {1,2} dan {3,4} sedangkan E berelemenkan 1,2,3 dan 4. Jadi {1,2},{3,4} adalah himpunan sedangkan 1,2,3,4 merupakan elemean. Untuk lebih jelasnya lagi 1 dan {1} berbeda karena 1 adalah elemen dan {1} adalah himpunan
Sekarang misalkan kita punya himpunan {a},{{a}} dan { {{a}} }
Apakah {a}={{a}}={{{a}}}?
Tentu tidak {a} berelemenkan a , {{a}} berelemankan himpunan {a}. dan { {{a}} } berelemenkan himpunan {{a}}. Selanjutnya kita peroleh:
|{a}|=1
|{ a,{a} }|=2
|{ a,{a},{{a}} }|=3
|{ a.{a},{{a}},{{{a}}} }|=4
karena {a}≠{{a}}}≠{{{a}}}
Himpunan juga boleh tidak mempunyai isi atau elemen, yang disebut himpunan kosong yang dinotasikan {Ø} dengan |{Ø}|=0
nah sekarang apakah {Ø}={{Ø}}?
Tentu saja tidak {Ø} himpunan kosong sedangkan {{Ø}} himpunan berelemenkan {Ø} itu artinya |{{Ø}}|=1
nah sekarang kita peroleh
{Ø} → 0
{{Ø}} → 1
{ {Ø},{{Ø}} } → 2
{ {Ø},{{Ø}},{{{Ø}}} } → 3
{ {Ø},{{Ø}},{{{Ø}}},{{{{Ø}}}} } → 4
.
.
.
.
{ {Ø},{{Ø}},{{{Ø}}},{{{{Ø}}}}…… } → n
Jadi menurut matematika kita bisa membuat/mengkontruksikan himpunan yang tak hingga banyaknya padahal himpunan tersebut sebenarnya kosong. Dengan matematika kita bisa membuat yang kosong menjadi tak hingga banyaknya padahal yang tak hingga banyaknya tersebut adalah kosong.
Nah sekarang kalian mengertikan makna dari “isi adalah kosong, kosong adalah isi”
atau kalian malah bingung
———————————————————————————————————————————————-r
Boleh dibilang ini adalah lanjutan dari part sebelumnya, saya akan melanjutkan bagaimana matematika memandang konsep “isi adalah kosong, kosong adalah isi”. Nah..pernahkah kalian bertanya/berpikir
Berapa sich hasil penjumlahan dari SEMUA bilangan real?
atau dengan kata lain
Berapa
Bagaimana kalo saya bilang hasilnya nol. Yup..semua bilangan kalo dijumlahkan hasilnya adalah nol.
Lho kok bisa?
Kita tahu bahwa himpunan bilangan real merupakan gabungan dari himpunan bilangan positif, himpunan bilangan negatif, dan singleton nol
denagan himpunan bilangan positif dan himpunan bilangan positif. Nah sekarang jumlahkan semua bilangan didalam himpunan bilangan positif
atau dengan cara yang lebih sederhana akan saya tulis
***
Didalam teori himpunan nol menunjukan banyaknya elemen didalam himpunan kosong





1 comments
Budhha memberkati
Post a Comment
Mari tinggalkan komentar yang baik dan benar